Simple Bayes Calculator
About this calculatorThis calculator allows you to enter your own numbers to perform simple Bayesian updating of an hypothesis in the light of new evidence.
There are plenty of simple calculators like this elsewhere on the internet. The advantage of this one is that its layout reflects in a somewhat more intuitive way the structure of a Bayesian inference, starting with prior probabilities on the left and moving to a posterior probability on the right. Along the way, it displays the calculations in a way that mirrors standard formulations of Bayes' theorem. Notice how the three boxes under "Bayesian Math" mirror the three main sections of the formula at right. |
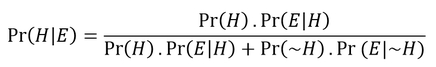
There are various forms or flavours of the theorem. The calculator above uses a standard form in which we effectively consider just one hypothesis (H) in relation to a single piece of evidence (E).
|
Instructions
Enter into the white boxes values describing the situation you are interested in, including labels for the primary and alternate hypotheses and the evidence. All other values are calculated automatically.
Note:
Note:
- probability values are entered as percentages
- the posterior probability will not be meaningful until you have entered values for both prior probabilities and both likelihoods.
Definitions
Primary & Alternate Hypothesis
These are the hypotheses whose probability is being revised in the light of the evidence. Usually the alternate hypothesis will be negation of the primary hypothesis, e.g.
Prior Probability
This is the probability of a hypothesis before the current piece of evidence, E, is taken into account.
In some contexts, such as the medical example below, the prior probability taken to be the same thing as the base rate of events of the kind described in the primary hypothesis.
Likelihood
This is the conditional probability of the evidence, given the hypothesis, written Pr(E|H). Put another way, it is the probability that you'd get the evidence if the hypothesis was true.
The likelihood of the primary hypothesis can also be considered the true positive rate. The likelihood of the alternate hypothesis is the false positive rate.
In a diagnostic testing context, where the primary hypothesis is that a patient has a certain condition, and the evidence a positive test for that condition, the likelihood of the primary hypothesis is the same as the sensitivity of the test.
In a diagnostic testing context, the likelihood of the alternate hypothesis is not the specificity of the test. Rather, specificity is the true negative rate, so the likelihood of the alternate hypothesis is the flip side of this, i.e. 1 minus the specificity.
Weighted Likelihood
The green boxes in the calculator, which all have the same value, contain the weighted likelihood of the evidence given the primary hypothesis, i.e. the probability of the evidence multiplied by the prior probability.
The reddish boxes are the weighted likelihood of the evidence given the alternate hypothesis.
Posterior Probability
The posterior probability of the primary hypothesis is the same thing as conditional probability of the hypothesis given the evidence. According to Bayes' Theorem, and as illustrated by the simple division appearing under "Bayesian Math" in the calculator, the posterior probability is equal to
These are the hypotheses whose probability is being revised in the light of the evidence. Usually the alternate hypothesis will be negation of the primary hypothesis, e.g.
- Primary: the patient has cancer (H)
- Alternate: the patient does not have cancer (~H)
- Primary: the suspect escaped by foot
- Alternate: the suspect escaped by vehicle
Prior Probability
This is the probability of a hypothesis before the current piece of evidence, E, is taken into account.
In some contexts, such as the medical example below, the prior probability taken to be the same thing as the base rate of events of the kind described in the primary hypothesis.
Likelihood
This is the conditional probability of the evidence, given the hypothesis, written Pr(E|H). Put another way, it is the probability that you'd get the evidence if the hypothesis was true.
The likelihood of the primary hypothesis can also be considered the true positive rate. The likelihood of the alternate hypothesis is the false positive rate.
In a diagnostic testing context, where the primary hypothesis is that a patient has a certain condition, and the evidence a positive test for that condition, the likelihood of the primary hypothesis is the same as the sensitivity of the test.
In a diagnostic testing context, the likelihood of the alternate hypothesis is not the specificity of the test. Rather, specificity is the true negative rate, so the likelihood of the alternate hypothesis is the flip side of this, i.e. 1 minus the specificity.
Weighted Likelihood
The green boxes in the calculator, which all have the same value, contain the weighted likelihood of the evidence given the primary hypothesis, i.e. the probability of the evidence multiplied by the prior probability.
The reddish boxes are the weighted likelihood of the evidence given the alternate hypothesis.
Posterior Probability
The posterior probability of the primary hypothesis is the same thing as conditional probability of the hypothesis given the evidence. According to Bayes' Theorem, and as illustrated by the simple division appearing under "Bayesian Math" in the calculator, the posterior probability is equal to
- the weighted likelihood of the evidence given the primary hypothesis divided by the sum of the weighted likelihood of the evidence given both hypothesis; or, put another way,
- the proportion of all positives which are true positives
Example
As discussed in this New York Times article, Gerd Gigerenzer has posed this medical diagnostic problem:
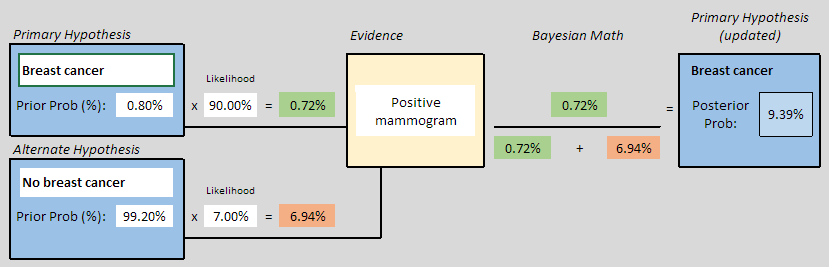
The probability that one of these women has breast cancer is 0.8 percent. If a woman has breast cancer, the probability is 90 percent that she will have a positive mammogram. If a woman does not have breast cancer, the probability is 7 percent that she will still have a positive mammogram. Imagine a woman who has a positive mammogram. What is the probability that she actually has breast cancer?
These values yield a probability of cancer of 9.39%, as shown in this screenshot:
The probability that one of these women has breast cancer is 0.8 percent. If a woman has breast cancer, the probability is 90 percent that she will have a positive mammogram. If a woman does not have breast cancer, the probability is 7 percent that she will still have a positive mammogram. Imagine a woman who has a positive mammogram. What is the probability that she actually has breast cancer?
These values yield a probability of cancer of 9.39%, as shown in this screenshot: